4. Nichtlineare Erweiterungen des Richardsonmodells

Das Modell von Richardson ist das berühmteste und wichtigste Modell der Konfliktforschung. Auf ihm basieren zahlreiche andere Modelle, die seine Idee verwendet haben. Richardson selbst hat sein Modell im Jahr 1939 nichtlinear erweitert und ausgebaut zum sogenannten Unterwürfigkeitsmodell. Von den anderen Varianten in der Literatur will ich jedoch nur eine herausgreifen und näher betrachten, nämlich das Modell von W. R. Caspary⁹.

4.1 Das Unterwürfigkeitsmodell

4.1.1 Die Modellgleichungen

Wie der Name schon andeutet, geht es in diesem Modell um die mathematische Deutung der Unterwürfigkeit. Damit ist die Tatsache gemeint, daß in einer Konfliktsituation der Schwächere von vornherein aufgibt, weil er sich dem übermäßig starken Gegner nicht gewachsen fühlt. Auf einer solchen Strategie bauen die rüstenden Nationen auf, wenn sie auf die Stellung eines besonders stark gerüsteten Imperiums hinarbeiten und die anderen Staaten durch ihre Übermacht völlig einschüchtern wollen. Das funktioniert jedoch nur, wenn diese Übermacht wirklich überwältigend groß ist.

Wie im ursprünglichen Modell von Richardson sollen auch hier die Rüstungsausgaben des ersten Staates x heißen, die des zweiten y.

Die Formulierung der Modellgleichungen unterlag mehreren Kriterien. Zunächst einmal sollte die Waffenebene (der positive Quadrant der (x, y)-Ebene) in der Aufteilung folgendermaßen beschaffen sein: In dem Gebiet um die x-Achse, wo die Werte von x sehr groß im Vergleich zu y sind, ist der zweite Staat eingeschüchtert und "unterwirft sich" dem ersten, indem er nicht mehr aufrüstet oder sogar abrüstet. Aber auch der erste Staat hat keine Veranlassung, weiter aufzurüsten. Die Bedrohung durch den zweiten Staat ist viel zu klein, um ernsthaft zu sein, die Aufrüstungsrate ist ebenfalls negativ. Aus Gründen der Symmetrie gelten diese Überlegungen auch für das Gebiet um die y-Achse. Nur um die erste Mediane bedrohen zwei gleichstarke Gegner einander und rüsten daher auf.

Weiters scheinen die linearen Gleichungen des ursprünglichen Systems um den Ursprung noch recht gut zu passen. Die neuen Gleichungen sollten keine Unstetigkeitsstelle in 0 haben, es soll also keine Terme mit x oder y im Nenner geben. Ob die militärische Stärke eines Staates den anderen wirklich einschüchtert, hängt nicht vom absoluten Stand seiner Rüstung ab, sondern vom Verhältnis von x zu y. Und schließlich sollen die Gleichungen nicht zu kompliziert sein, sodaß sie sich noch relativ leicht beschreiben und untersuchen lassen.

Die Differentialgleichungen, die Richardson fand, lauten:

(4.1)

(4.2)

Die Parameter k, l, a, b, g und h haben hier die selbe Bedeutung wie in (1.20). Die neuen Parameter r und s bringen die Unterwürfigkeit in das Modell. Wir setzen wieder voraus, daß alle Parameter positiv sind. Dieses Modell ist eine echte Erweiterung des ursprünglichen, denn bei r = s = 0 haben wir die Gleichungen (1.18) und (1.19), und die Modelle sind identisch.

Wie wird nun der Effekt der Unterwürfigkeit modelliert? Der konstante Bedrohungskoeffizient wird multiplikativ um einen Ausdruck erweitert, der von der Differenz der vorhandenen Rüstung beider Staaten abhängt. Dieser Faktor, der vor dem y in (4.1) steht, kann positiv oder negativ sein. Wenn x > y ist, so ist er positiv, ebenso wenn x < y < x + 1/r. Der Ausdruck vor dem x in (4.2) ist positiv wenn x > y einerseits oder wenn x > y > x - 1/s.

Damit ist aber noch nicht geklärt, ob der Staat nun wirklich aufrüstet. Wenn (1 - r×(y -x)) < 0 ist, also y > x + 1/r und damit y viel größer als x ist, so beherrschen die negativen Koeffizienten die rechte Seite der Differentialgleichung. Der erste Staat "unterwirft sich" und rüstet ab. Ist dieser Ausdruck positiv, aber y nicht viel größer im Vergleich zu x, dann ist -a×x der Summand, der das Vorzeichen von bestimmt, und wiederum rüstet der erste Staat ab. Es wird nur aufgerüstet, wenn der Ausdruck k×(1 - r×(y -x))×y positiv und sehr groß ist, -a×x aber nicht so groß. Dieser Fall tritt ein, wenn y » x. Das ist genau das Verhalten, das zu erreichen war.

4.1.2 Gleichgewichtslagen und Stabilität

Die Gleichgewichtslagen werden bestimmt, indem = = 0 gesetzt wird. Es ergeben sich zwei Gleichungen, die Terme in 1, x, y, x², y² und x×y enthalten. Sie sind nicht so ohne weiteres zu lösen, also betrachten wir ihre Struktur genauer und versuchen daraus ein Ergebnis abzulesen.

(4.3)

(4.4)

Das sind eindeutig Gleichungen von Kegelschnitten. Wir müssen also ihre Invarianten betrachten und daraus die Art der Kurve bestimmen. Die Invarianten eines Kegelschnittes sind die zwei Determinanten, die aus den Koeffizienten der Gleichung gebildet werden.

(4.5)

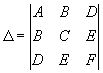(4.6)

(4.7)

Wie sehen die Invarianten für unsere beiden Gleichungen aus? Wir müssen nur die entsprechenden Koeffizienten aus (4.3) und (4.4) in die Determinanten einsetzen.

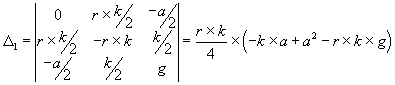(4.8)

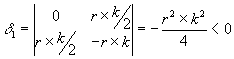(4.9)

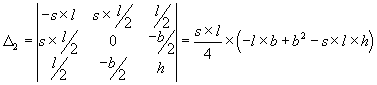(4.10)

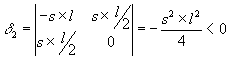(4.11)

Jedes d_i ist negativ, das bedeutet, daß es sich entweder um eine Hyperbel handelt, wenn der Kegelschnitt ein eigentlicher ist und D_i ¹ 0, oder um zwei einander schneidende Gerade, wenn D_i = 0 und der Kegelschnitt entartet. Damit haben wir vier Fälle, die gesonderter Untersuchung bedürfen.

Abbildung 4.1 Übersicht der zu behandelnden Fälle
	D₁ = 0	D₁ ¹ 0
D₂ = 0	Fall 1	Fall 3
D₂ ¹ 0	Fall 2	Fall 4

1. Fall: Zwei Geradenpaare

In diesem Fall entarten beide Kegelschnitte zu je zwei Geraden, die einander schneiden. Zunächst gilt es, die Werte von r und s zu ermitteln, für die D₁ = 0 und D₂ = 0 sind, dann müssen wir die Geradengleichungen finden, indem wir (4.3) und (4.4) als Produkt zweier in x und y linearer Ausdrücke ansetzen, und schließlich können die Schnittpunkte berechnet werden. Wir bestimmen also zuerst r und s aus (4.8) und (4.10).

(4.12)

(4.13)

(4.14)

(4.15)

Diese Werte von r und s setzen wir in (4.3) und (4.4) ein und erhalten Gleichungen in x, x², y, y² und x×y, die sich als Produkt zweier Ausdrücke in x und y darstellen lassen. Mit einem unbestimmten Ansatz und anschließendem Koeffizientenvergleich bestimmen wir die Gleichungen der Geraden. Bei diesem Ansatz hat jeweils ein Faktor schon spezielle Gestalt, denn die Terme x² und y² treten nie gemeinsam auf. Dadurch läßt sich die Rechnung vereinfachen.

(4.16)

(4.17)

Die beiden Paare einander schneidender Gerade sind also:

(4.18)

(4.19)

(4.20)

(4.21)

Zunächst sehen wir, daß (4.18) und (4.20) den gleichen Anstieg haben, nämlich 1. Das bedeutet, daß die beiden Geraden einander nicht schneiden. Es bleiben noch drei weitere Schnittpunkte zu berechnen, die Gleichgewichtslagen sind. ist der Schnittpunkt von (4.18) mit (4.21), der Schnittpunkt von (4.19) mit (4.20) und der Schnittpunkt von (4.19) mit (4.21).

(4.22)

(4.23)

(4.24)

Ob diese Gleichgewichtslagen nun stabil sind oder nicht, kann uns vielleicht eine Skizze der Geraden und ihrer Schnittpunkte sagen. Es gibt verschiedene Möglichkeiten, wie die Geraden liegen können. (4.18) ist einer Gerade mit dem Anstieg 1 und schneidet die y-Achse unterhalb des Ursprungs, (4.19) ist eine waagrechte Gerade, die oberhalb der x-Achse verläuft, wenn k - a > 0 ist. Das wollen wir voraussetzten, weil wir nur an Schnittpunkten im ersten Quadranten interessiert sind. Aus dem selben Grund lassen wir die senkrechte Gerade (4.21) rechts von der y-Achse verlaufen, also l - b > 0 sein. Von (4.20) wissen wir, daß sie die y-Achse oberhalb des Urprungs schneidet und parallel zu (4.18) liegt. So erhalten wir drei prinzipielle Möglichkeiten. Die Geraden (4.18) bis (4.211) sind mit den römischen Ziffern I bis IV gekennzeichnet, die Ebene wird durch sie in verschiedene Gebiete geteilt, in denen die Werte von und sowohl positiv als auch negativ sein können. Dadurch ergeben sich die prinzipiellen Richtungen von Trajektorien.

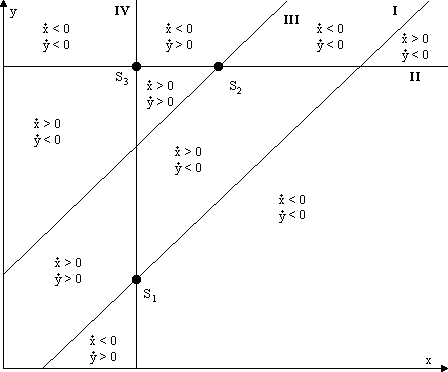
Abbildung 4.2 Lage der Geraden, Fall A

Im Fall A liegen die Geraden so, daß sich der Schnittpunkt S₃ links von S₂ und oberhalb von S₁ befindet. Es gibt noch den Fall B, wo sich S₃ rechts von S₂ und oberhalb von S₁ befindet sowie den Fall C, wo S₃ rechts von S₂ und unterhalb von S₁ liegt.

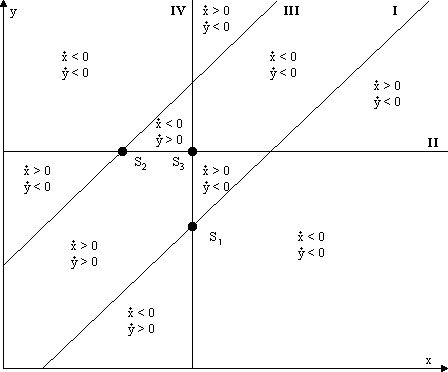
Abbildung 4.3 Lage der Geraden, Fall B

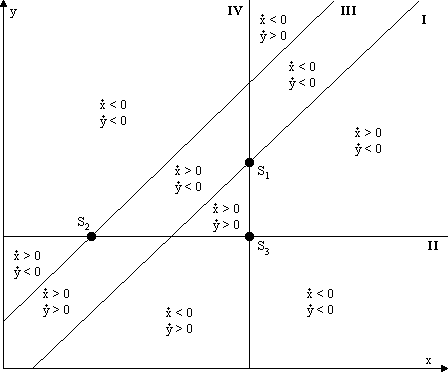
Abbildung 4.4 Lage der Geraden, Fall C

Im Fall A zeigt sich, daß S₂ nicht stabil sein kann. Um S₁ und S₃ laufen die Trajektorien spiralförmig, wobei noch zu klären ist, ob sie sich diesen Punkten nähern oder von ihnen entfernen. Der Verlauf der der Trajektorien um S₁ ist jedenfalls im Uhrzeigersinn, um S₃ im Gegenuhrzeigersinn. Das läßt sich aus der Skizze ablesen. Im Fall B ist S₁ der Punkt, der im Uhrzeigersinn umlaufen wird, und S₂ der, der im Gegenuhrzeigersinn umlaufen wird. S₃ ist eindeutig instabil. Schließlich gibt es noch den Fall C, in dem S₃ im Uhrzeigersinn umlaufen wird und S₂ im Gegenuhrzeigersinn, und S₁ instabil ist. Welcher der untersuchten Punkten tatsächlich stabil ist, bleibt noch durch Simulation in HYBSYS zu untersuchen.

2. Fall Zwei Gerade und eine Hyperbel

Unsere Voraussetzungen sind jetzt, daß D₁ = 0 ist, aber D₂ ungleich 0. Es gelten also die Geradengleichungen (4.18) und (4.19) sowie die Hyperbelgleichung (4.4). Die Gleichgewichtslagen sind die Schnittpunkte dieser Kurven. Sie haben folgende Koordinaten:

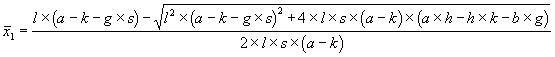(4.25)

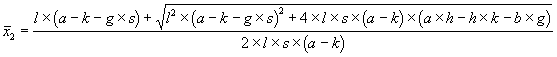(4.26)

(4.27)

(4.28)

(4.29)

Wie sehen hier, daß die Gerade (4.19) die Hyperbel zweimal schneidet, die Gerade (4.18) aber nur einmal. Es gibt also drei Gleichgewichtslagen.

Zunächst betrachten wir die Hyperbel (4.4) etwas genauer. Die Gleichung weist die Besonderheit auf, keinen Term mit y² zu enthalten. Es ist zu vermuten, daß sie daher eine spezielle Gestalt hat. Lösen wir zunächst die Gleichung nach y auf, das ja nur linear auftritt, so erhalten wir einen Bruch. Die Nullstelle des Nenners ist eine Unstetigkeit, ein Pol.

(4.30)

(4.31)

Das Verhalten von y = y(x), wenn x ® ¥, läßt sich ebenfalls bestimmen. In diesem Fall strebt y auch gegen ¥, und zwar mit dem Anstieg 1. Somit ist die Assymptote parallel zu der Geraden (4.18), und die Gerade schneidet die Hyperbel nur einmal.

(4.32)

Eigentlich waren diese Ergebnisse zu vermuten, denn die Assymptoten der Hyperbel, die wir durch (4.31) und (4.32) erhalten können, sind nichts anderes als die Geradengleichungen (4.20) und (4.21). Anstatt Skizzen zu produzieren, die denen aus Fall 1 sehr ähnlich wären, nutze ich die Ähnlichkeit um die Überlegungen identisch zu verwenden. Die Gebiete mit positiven und negativen Ableitungen in der (x, y)-Ebene liegen genauso wie in Abbildung 4.2 bis Abbildung 4.4, nur die Ränder sind ein wenig verschoben und gekrümmt. Die Hyperbel schmiegt sich an die Geraden (4.20) und (4.21) und folgt so in etwa ihrem Verlauf. An den wesentlichen Aussagen ändert der kleine Unterschied nichts.

3. Fall Eine Hyperbel und zwei Gerade

Der dritte Fall ist symmetrisch zum zweiten. Es gelten die Gleichungen (4.3) für die Hyperbel und (4.20) und (4.21) für die beiden Geraden. Die Schnittpunkte sind:

(4.33)

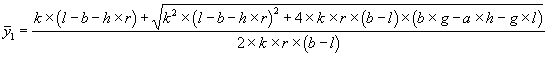(4.34)

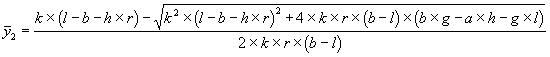(4.35)

(4.36)

(4.37)

Auch hier erübrigt sich eine Skizze, denn die Assymptoten der Hyperbel sind die Geraden (4.18) und (4.19).

4. Fall Zwei Hyperbeln

Im Fall von zwei Hyperbeln, die den Gleichungen (4.3) und (4.4) genügen, wird die Berechnung der Gleichgewichtspunkte schwierig. Da wir aber in den Fällen 2 und 3 einiges über die spezielle Gestalt der Hyperbeln herausgefunden haben, gestaltet sich die theoretische Betrachtung anhand von Skizzen einfach. Da dieser Fall der allgemeinste ist, möchte ich hier wieder die drei Möglichkeiten skizzieren.

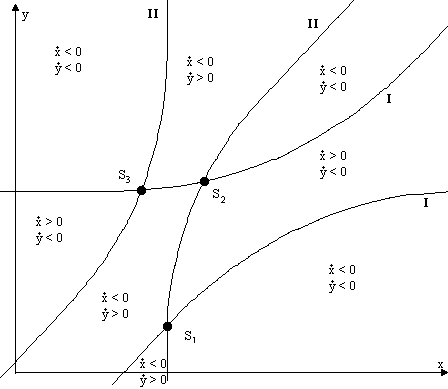
Abbildung 4.5 Lage der Hyperbeln, Fall A

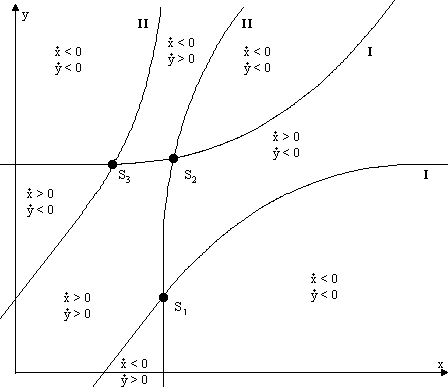
Abbildung 4.6 Lage der Hyperbeln, Fall B

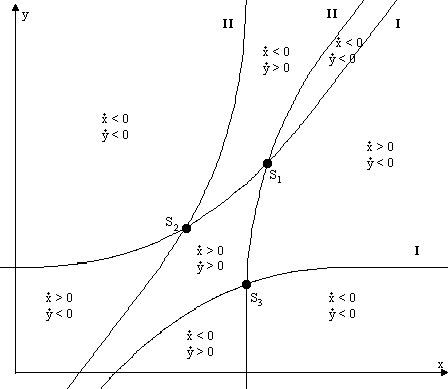
Abbildung 4.7 Lage der Hyperbeln, Fall C

4.1.3 Implementation und Ergebnisse

Die Simulation mit HYBSYS zeigt, daß das Modell eine stabile Gleichgewichtslage besitzt. Die Rüstungsausgaben x und y schwanken zunächst zwischen mehreren lokalen Extremwerten, deren Abstand jedoch rasch abnimmt, und bleiben dann auf einem festen Wert. In den Phasenbildern wirkt sich das so aus, daß die Trajektorien spiralförmig dem Gleichgewichtspunkt zustreben.

Mit Hilfe der Simulation läßt sich feststellen, ob und welche der Gleichgewichtspunkte stabil sind. Zunächst möchte ich aber die Bedingungen aufstellen, an denen wir erkennen, in welcher der drei besprochenen Lagen die Hyperblen wirklich liegen. Wenn wir statt der Hyperbeln aus dem allgemeinen Fall 4 die Geraden aus dem Fall 1 verwenden, so ändert sich an der relativen Lage der Schnittpunkte der Kurven nichts, aber wir erhalten einfache Ungleichungen für die Parameter der Differentialgleichung, die wir überprüfen können.

Fall A

Der Gleichgwichtspunkt S₁ liegt links von S₂ und oberhalb von S₃. Die entsprechenden Ungleichungen lauten:

(4.38)

(4.39)

(4.40)

(4.41)

Durch die Simulation mit Werten, die diesen Ungleichungen entsprechen, sehen wir deutlich, daß ein Gleichgewichtspunkt stabil ist, nämlich S₁.

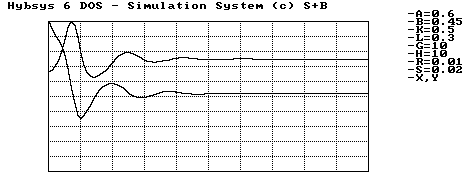
Abbildung 4.8 Fall A, stabile Gleichgewichtslage S₁

Die Abbildung 4.8 zeigt den Verlauf der Rüstung. Am Anfang gibt es starke Schwankungen, die durch die gegenseitige Unterwürfigkeit entstehen. Nach einiger Zeit erreichen beide Staaten ihre Gleichgewichtslage.

Die Abbildung 4.9 zeigt, wie die Trajektorien die Gleichgewichtslage erreichen. Die Spirale dreht sich im Uhrzeigersinn, und auch die Werte der Koordinaten bestätigen, daß S₁ der stabile Gleichgewichtspunkt ist.

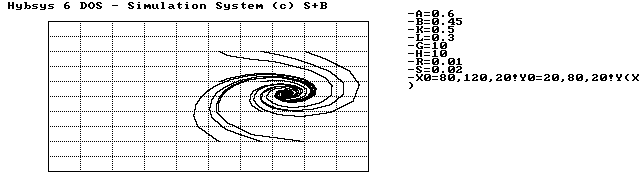
Abbildung 4.9 Fall A, Trajektorien zum stabilen Gleichgewichtspunkt S₁

Fall B

Der Punkt S₁ liegt rechts von S₂ und oberhalb von S₂. Es gilt daher die Ungleichung (4.41), aber die Umkehrung von (4.39). Die Trajektorien verlaufen leicht im Uhrzeigersinn gedreht nach der stabilen Gleichgewichtslage S₁.

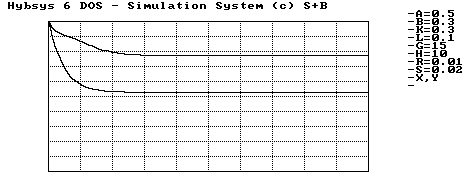
Abbildung 4.10 Fall B, stabiles Gleichgewicht S₁

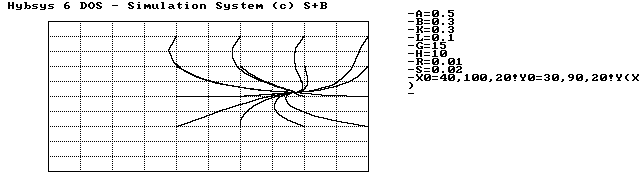
Abbildung 4.11 Fall B, Trajektorien zum stabilen Gleichgewichtspunkt S₁

Die Abbildung 4.10 zeigt, daß eine rasche Abrüstung erfolgt, die den Stand auf die stabile Lage bringt. Die Modellannahmen bringen also unter günstigen Vorausssetzungen mit den geeigneten Parametern die Rüstung schnell auf einen konstanten Wert.

Fall C

In diesem Fall sind die Ungleichungen (4.39) und (4.41) nicht gültig; die Ungleichheitszeichen drehen sich um. Die Simulation mit Werten, die den Bedingungen entsprechen, zeigt, daß die Trajektorien sich gegen den Uhrzeigersinn zur Gleichgewichtslage hin drehen. Also ist der Punkt S₂ stabil.

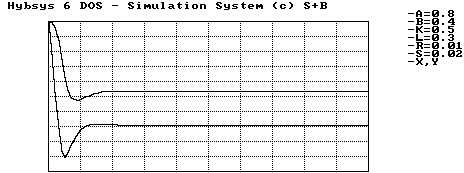
Abbildung 4.12 Fall B, stabiles Gleichgewicht S₂

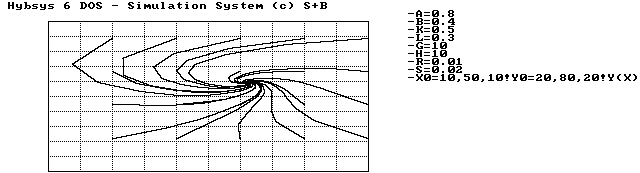
Abbildung 4.13 Fall B, Trajektorien zum stabilen Gleichgewichtspunkt S₂

4.1.4 Vergleich der Modelle

Das Unterwürfigkeitsmodell ist eine direkte Erweiterung des klassischen Modells von Richardson. Anstelle des Bedrohungsparameters ist ein Ausdruck getreten, der nicht mehr konstant ist. Dieser Faktor hängt von der Differenz der beiden Rüstungen ab. Auf diese Art modelliert Richardson den Zusammenhang zwischen den Staaten noch viel enger als in seinem ersten Modell. Wenn r = s = 0 sind, so erhalten wir die Gleichungen (1.18) und (1.19), oder anders ausgedrückt: das klassische Richardsonmodell verhält sich wie das Unterwürfigkeitsmodell, wenn die Werte der Rüstungsausgaben beider Staaten annähernd gleich sind. Im zweiten Modell gibt es jedoch immer einen stabilen Gleichgewichtspunkt, der nach einigen Schwankungen auch erreicht wird. So eine Schwankung hat Tiefpunkte, von denen aus die Kurven exponentiell anwachsen bis zu einem Wendepunkt. Dieser Teil der Kurve hat starke Ähnlichkeit mit dem exponentiellen Wachstum der Kurven im ersten Modell, wenn die Gleichgewichtslage nicht stabil ist. Das ständige exponentielle Rüstungswachstum ist ja schwer vorstellbar. Irgendwann kommt es zu Verhandlungen, die Rüstungsraten zu verringern; vielleicht kommt es auch zu Abrüstungsgesprächen. Könnte es sein, daß sich die beiden Großmächte USA und UdSSR in der Nähe dieses Wendepunktes befinden?

Im Vergleich mit den linearen Erweiterungen aus dem dritten Kapitel zeigt sich, daß das Unterwürfigkeitsmodell zwar für zwei Staaten allgemeiner modelliert, auf mehr Staaten aber nicht anwendbar ist. Es wäre aber denkbar, die Gleichungen so zu verändern, daß die Beteiligung eines dritten Staates möglich ist.

4.2 Das Modell von Caspary

4.2.1 Die Modellgleichungen

W. R. Caspary¹⁰ bringt zusätzliche ökonomische Überlegungen in das Modell von Richardson ein. Dadurch soll es realistischer werden. Es gibt für jeden Staat eine obere Schranke des für die Rüstung zur Verfügung stehenden Kapitals. Diese gesamte Summe ist eine Konstante, die für den einen Staat C heißen möge, für den anderen C'. Dieses Geld kann jedoch nicht zur Gänze für die Anschaffung neuer Waffen ausgegeben werden. Die bereits vorhandenen bedürfen der Wartung und Pflege, was Kosten verursacht. Sei m beziehungsweise m' die Größe der Kosten pro Einheit des vorhandenen Waffenpotentials. Für die Produktion oder den Ankauf neuer Waffen stehen dann zur Verfügung:

(4.42)

(4.43)

Die bekannten Differentialgleichungen von Richardson finden ihren Eingang in das neue Modell. Wir fassen die rechten Seiten von (1.18) und (1.19) unter einem neuen Namen zusammen.

(4.44)

(4.45)

Die letzten neuen Parameter sind p und p', die angeben, wie weit die Staaten in ihren Rüstungsausgaben von der bereits vorhandenen eigenen und fremden Rüstung abhängen. Das Modell erhält seine Gestalt einerseits durch die Überlegung der Beschränkung in den Ausgaben, andererseits durch die starke Bereitschaft, immer mehr Geld in die Rüstung zu stecken. So wird in kurzer Zeit die maximale Summe ausgegeben, die zur Verfügung steht.

(4.46)

(4.47)

Für kleine Werte von d und d' sind die Exponentialausdrücke fast 1, und und sind daher fast 0. Das ist das selbe Verhalten, wie es auch durch die linearen Differentialgleichungen von Richardson modellliert wird. Bei großen Werten von d und d' wird der Wert der zweiten Klammer fast 1, und die Beschränkung der Kosten durch C und C' kommt voll zur Geltung.

Der exponentielle Ausdruck läßt sich linearisieren, indem wir die Exponentialfunktion nach ihrer Taylorreihe entwickeln und nach dem linearen Glied abbrechen. So erhalten wir eine Näherungsformel, die um den Urprung nicht stark abweicht und sich leicht näher untersuchen läßt.

(4.48)

(4.49)

(4.50)

(4.51)

Die neuen Differentialgleichungen haben eine ähnliche Struktur wie der Fall 1 aus dem Unterwürfigkeitsmodell, nur die Koeffizienten sind allgemeiner, und wir können die rechten Seiten als "vertauscht" ansehen. Insofern ist dieses modifizierte Modell eine Art Erweiterung des Unterwürfigkeitsmodells und damit auch des Richardsonmodells. Durch die Fortführung der Exponentialreihe wird das Modell zum eigentlichen Casparymodell erweitert. Mit diesen Überlegungen zeigt sich, daß die Einführung der Exponentialfunktion nicht ganz willkürlich war.

4.2.2 Gleichgewichtslagen und Stabilität

Die Gleichgewichtspunkte lassen sich leicht berechnen. Es sind vier, und einer von ihnen ist der gleiche wie im Modell von Richardson mit den Koordinaten (1.29) und (1.30). Sie sind die Schnitttpunkte folgender Geraden, die sich durch Gleichsetzung von und mit 0 ergeben.

(4.52)

(4.53)

(4.54)

(4.55)

(4.56)

(4.57)

(4.58)

(4.59)

(4.60)

(4.61)

Durch die Modellannahmen, die Beschränkung der Kosten, gibt es keinen Fall von unbeschränktem Wachstum. Es kann daher nicht sein, daß keine der Gleichgewichtslagen stabil ist.

Die Frage der Stabilität können wir wieder anhand von Skizzen erörtern. Allerdings gibt es mehr Möglichkeiten, wie die Geraden liegen können, als im Unterwürfigkeitsmodell, weil die beiden schrägen Geraden nicht parallel sind. Von den vielen Möglichkeiten möchte ich jedoch nur vier herausgreifen, und zwar ohne Information zu verlieren. Jede Gleichgewichtslage hat die "Chance", stabil zu sein, und in jedem der vorgestellten Fälle gibt es eine stabile Gleichgewichtslage. In den vier verschiedenen Skizzen sind alle vier verschiedenen Punkte einmal stabil.

Die Geraden (4.52) bis (4.55) sind in den Skizzen mit den römischen Ziffern I bis IV bezeichnet.

Im Fall A ist der Punkt S₁ stabil. Das zeigt sich dadurch, daß die Richtungen der Trajektorien auf ihn weisen. Die Abbildung 4.14 veranschaulicht, wie die vier Geraden liegen, und in welche Gebiete sie die Ebene teilen. Die Vorzeichen von x und y ändern sich an den entsprechenden Geraden (4.52) bis (4.55), und so hat jedes Gebiet eine Vorzugsrichtung, in der die Trajektorien laufen, solange sie sich innerhalb des Gebiets befinden. Diese Richtung ist bei den vier Gebieten um S₁ herum die nach S₁.

In Fall B ist S₂ der stabile Gleichgewichtspunkt. Die Skizze zeigt, wie die Trajektorienrichtungen liegen, sodaß sie diesen Punkt direkt anstreben. Wenn die Gleichgewichtspunkte so liegen wie in Abbildung 4.15, so ist S₃ stabil, das ist der Fall C. Schließlich gibt es auch noch die Möglichkeit, daß S₄ stabil ist.

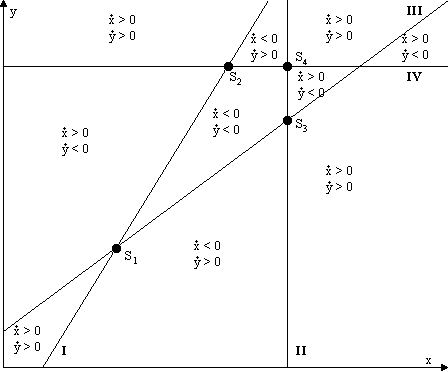
Abbildung 4.14 Stabiler Gleichgewichtspunkt S₁, Fall A

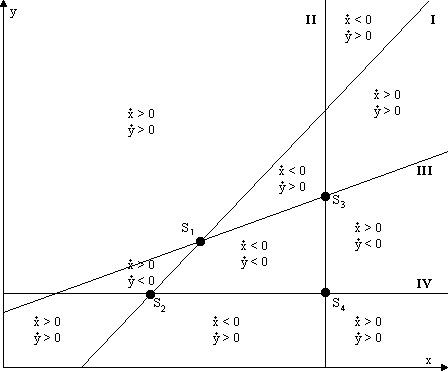
Abbildung 4.15 Stabiler Gleichgewichtspunkt S₂, Fall B

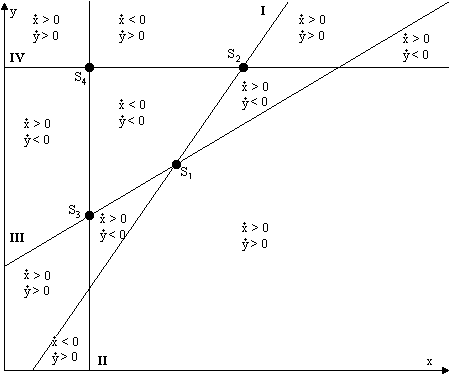
Abbildung 4.16 Stabiler Gleichgewichtspunkt S₃, Fall C

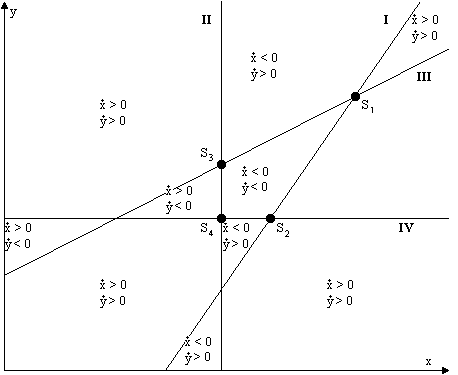
Abbildung 4.17 Stabiler Gleichgewichtspunkt S₄, Fall D

4.2.3 Implementation und Ergebnisse

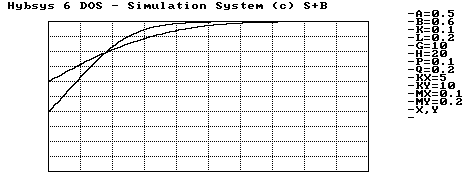
Abbildung 4.18 Rüstungsverlauf nach Caspary

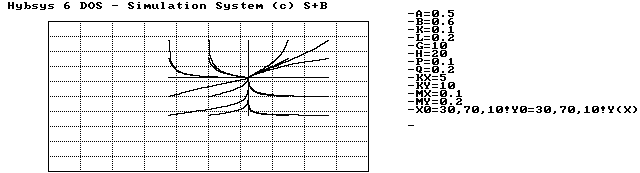
Abbildung 4.19 Verlauf der Trajektorien nach Caspary

Die Bilder, die das Modell hervorbringt, ähneln einander stark. Da es in jedem Fall einen stabilen Wert gibt, streben die Waffenpotentiale gegen ihn, und zwar so direkt wie möglich. Am Anfang wird rasch aufgerüstet, bald aber zeigt sich die Beschränkung der Finanzen, die Kurven flachen zusehends ab und erreichen die stabile Gleichgewichtslage. Das Phasenbild zeigt auch einige Trajektorien, die ganz gerade dem Gleichgewichtspunkt zustreben. Egal, welcher Gleichgewichtspunkt der stabile ist, die Art der Kurven ändert sich nicht.

4.2.4 Vergleich der Modelle

Wie schon in 4.2.1 gezeigt wurde, ist dieses Modell eine wirkliche, direkte Erweiterung des Richardsonmodells. Die Exponentialfunktion wirkt zunächst vielleicht aus der Luft gegriffen, aber als Reihe betrachtet ist sie die Fortsetzung des linearen Ausdrucks des Richardsonmodells. Zum direkten Vergleich möchte ich die Differentialgleichungen der speziellen Fälle von 2.1.2 und 2.2.2 direkt untereinanderschreiben, und die Waffenansammlungen zur Unterscheidung mit den Indizes u für Unterwürfigkeit und c für Caspary versehen. Wir sehen deutlich die starke Ähnlichkeit der beiden Modelle.

(4.62)

(4.63)

(4.64)

(4.65)

Im Vergleich zu den linearen Erweiterungen aus Kapitel 3 ist das Modell von Caspary zwar nur für zwei verfeindete Staaten gültig, erhebt aber Anspruch darauf, daß seine Gleichungen realistischer sind. Sogar das exponentielle Wachstum, das bei großen Bedrohungsparametern und kleinen Sättigungsparametern in den linearen Modellen auftritt, läßt sich interpretieren als der anfänglich steile Anstieg der Kurven bei Caspary, die jedoch infolge der finanziellen Beschränkungen hier irgendwann wieder abflachen. So wie sich das bekannte biologische Modell des logistischen Wachstums als realistischer als das des unbeschränkten Wachstums herausgestellt hat, so könnte auch das Modell von Caspary das von Richardson überholt haben.

Kurzfassung und Inhaltsverzeichnis
Einleitung
1. Das Modell von Richardson
2. Das Modell von Intriligator und Brito
3. Lineare Erweiterungen des Richardson-Modells
4. Nichtlineare Erweiterungen des Richardsonmodells
5. Nichtlineare Erweiterung des Intriligator-Brito-Modells
Literaturverzeichnis